Rate and Master Equations
Table of Contents
Introduction
This is part 1/? of a series of posts on the theory of “reaction networks”, a.k.a. “Petri Nets”, a.k.a. “mass-action kinematics”. For the most part this material will be assembled from various links on John Baez’ page. Almost nothing here is my own work, but I will be restating it in my own words and partially in my own notation.
My own interests are in:
- Elementary examples of parts of quantum-mechanics and statistical-mechanics, e.g. Fock Space, and in decomposing these theories into simpler ones.
- The relationships between descriptions of the same system at levels of abstraction, with a renormalization flavor.
- The zoo of equilibrium behaviors of dynamical systems, and how they relate to the underlying parameters
- Generating function methods, wherever they appear.
- The opportunity to develop methods of diagramming high-dimensional spaces.
Reaction Networks
A “reaction network” is a graph whose edges represents “reactions” (or “processes” or “transitions”) between different “complexes” (or “combinations” or “tuples”) of “species”, each with an associated “rate constant”. For example:
The standard examples of systems which might be described by reactions networks are:
- Chemicals, where the “species” stand for molecules, and reactions stand for reactions.
- Population dynamics, where the “species” represent species, or cells, enzymes, viruses, etc, and reactions stand for interactions between species, like predation or asexual reproduction.
A reaction network represents the set of processes that can change the state of a many-particle system. Only these reactions can occur, and no others; therefore any state which is not accessible via some sequence of reactions is unreachable. The set of possible states is further constrained by the rate constants: some states may turn out to be attractors, others dynamically unreachable. The second reaction above represents a reversible reaction, so in principle this system could move back and forth along the line of
Levels of Abstraction
I want to emphasize at the outset that a reaction network merely describes a set of processes, which can be “translated” into equations in different ways—in particular, at different “resolutions”, “levels of analysis”, or “levels of abstraction”. 0. Equilibrium. The highest level of abstraction. Here we characterize a system by its equilibrium or long-time behaviors, which might be an attractor state, but also might include more complicated behaviors like cycles. Whether these states can be deduced from the network is a matter of mathematics.
Examples: Thermodynamics as equilibrium stat-mech. Expectations of stationary wave functions in quantum mechanics.
-
Expectations. This is the entrypoint for most analysis of a reaction network: we translate the network into differential equation in the average populations or concentrations. This is called “Rate Equation”, which is an ODE for species averages
. It can be analyzed for long-time behavior and for stability and bifurcations, etc, which can tell us things at level 0. Examples: in quantum mechanics: the classical limit as an expectation, or in another sense, stationary wave functions. Various models one encounters in diff-eq class, like the predator-prey model and various models of viral spread.
-
Stochastic Dynamics. At this much-lower level of abstraction, we can describe the system as a probability distribution over states with exact numbers of each species. Then we can translate our reaction network into a differential equation for the evolution of this probability distribution, giving a “stochastic dynamical system”. This level gives a better picture of the underlying behavior, but is much higher-dimensional and correspondingly is much harder to solve. Nonetheless, under some conditions we can characterize equilibrium solutions at this level of analysis, and can lift these solutions to the Rate-Equation level.
Examples: the Shrodinger equation, especially when viewed as a path integral of a propagator.
-
Histories, Timelines, or Sequences of Reactions. At a lower-level still would be a characterization of the state as a particular sequence of reactions, with which we can associate some probability-weight or “amplitude”. The weighted sum of all possible timelines we expect to leads to the higher-level characterizations of the system. But this level of analysis is particularly suited to questions like: what is the probability for a transition between specific starting and ending states?
Examples: a diagram in a path integral, in QFT. I also think of “programs”, in the sense of a sequence of expressions in an abstract language. Or, the probability of a specific sequence of mutations occuring in genetics, and the ways that selection effects would bias the post-hoc distribution of mutations. Or, the probability that some system breaks down over time.
-
Micro-scale Dynamics. At the lowest level of analysis we have the interactions of individual particles. At this level the reaction network doesn’t tell us anything; in fact this is the level where you might calculate the rate constants used at higher levels of analysis by computing scattering cross sections from the underlying dynamics. Or perhaps we can use statistical-mechanics methods to find a density-of-states or partition function.
Examples: Hamiltonian mechanics of interacting particles in a gas. Individual vertexes in QFT.
Most of the theory here will concentrate on the three highest levels of analysis. In particular, we’ll want to say things about the behavior at higher levels of abstraction, through arguments at lower levels.
I spell all of this out because, first, I think it will be a good way to organize these ideas, but in particular because, for me, the most interesting thing about reaction networks is as a model system for understanding the relationships between the different levels of abstraction.
Level 1: The Rate Equation
Anatomy of a Rate Equation
A reaction network is most simply seen as encoding a differential equation called the “Rate Equation” of the network.
Here is the example from above again:
We translate into the following set of coupled diff-eqs:
When we want to iterate over reactions, we’ll index by
The rate of a reaction depends on the product of the concentrations of its inputs only, e.g. our first reaction
The coefficients like
The groups of species appearing on either side of the reactions are the “complexes” of the network.
We will index complexes by a lower-case
, so , , and the full tuple is . , so and the full tuple is .
The difference
We could try to write the Rate Equation as a matrix equation:
…but this won’t be very useful because the matrix isn’t square—instead it has dimension
The Rate Equation in Tuple Notation
We can condense the Rate Equation somewhat by summing over reactions, where
This is not too bad, but all those species indices are not so easy to read. Some of the literature chooses to clean this up by omitting the species index entirely, asking us to remember which terms refer to species (which obey special rules_) and which do not. I want to take a different approach and represent all indexing-over-species as an overbar
A tuple over species
Tuples can be added or subtracted, and it will occasionally be useful to take a dot-product:
We’ll also define operations on tuples which do not have vector analogs. Most operations which would not be defined on vectors we implement by applying component-wise, then multiplying all of the components of the result:
Note that the last line is a succinct way to write a multinomial coefficient
Finally we will need a couple more non-standard operations. First we have the “falling power”, which works for integers or tuples:
The last line indicates that the falling power could be related to a multinomial coefficient with both arguments tupled, but this seems a little too wacky, so we won’t use it.
Note that
Next we have the scalar product of more-than-2 tuples, which we write as a chain of dot-products:
And lastly we implement inequality between tuples, which can be seen as a shorthand for “logical AND” or as a product of indicator functions. We won’t attempt to find a notation for “OR”.
With all of this notation, and
We want to write this as a “tuple equation”, just as we do for vectors, representing a system with one equation for each index
We immediately encounter a weakness of the notation, unfortunately—we would like to write this term as
An alternative to all of this would be to use an Einstein-like notation, with the rule that tuple components multiply for any tuple index appearing on only one side of the
I’m going to stick with tuples, though—we’ll get a lot of use out of them.
Our concise Rate Equation is therefore:
A Rate Equation Example
For any particular network you could attack the corresponding Rate Equation with the methods of standard differential equations. In general we can’t hope to find exact solutions; the goal of such analysis is usually to make “level 0” statements characterizing equilibria and long-time behavior. But it will be helpful to see the general shape such an analysis takes with a worked example.
As a demonstration of what it takes to analyze a particular Rate Equation, I’ll look at the following simple model of an epidemic, where
This leads to the following system of equations:
The
For such simple system the tuple notation is no help at all, and the clearest form would would probably be to just expand the “input” tuples:
Clearly the total population
Now we’ll solve this. This system is simple enough that it admits an exact solution by way of the following trick. We observe that the
Then the solutions for
And we can make use of the fact that
We now define parameters to make this dimensionless. If we define
And now we define constants
We arrive at a fairly simple first-order differential equation, which is most easily analyzed by observing that
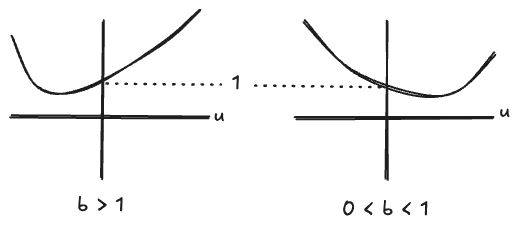
Then the full system
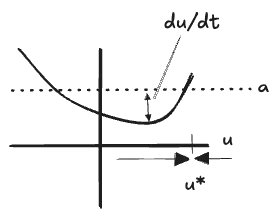
Apparently:
- When
- When
From here you could go on to calculate the location of the fixed point as a function of the parameters and the initial conditions, or the timescale of convergence to the fixed point, or you could modify this comically-simple model to include behaviors like “getting better” and “quarantining”. But it is adequate to demonstrate the typical behavior of reaction networks: fixed points appear and move around the parameter space as a function of the rate constants.
Level 2: The Master Equation
Stochastic Evolution
In one sense the Rate Equation is a direct translation of the information in a reaction network. But in most cases this should be thought of as an approximation of the underlying physical system, in a few ways:
- The rate constants
- The law that reactions occur with rate
- The initial conditions are only approximate measurements and therefore represent a peaked distribution of species numbers
We could imagine trying to “undo” the abstraction along any of these axes. Here we’ll take the first two as givens—as assumptions of the “reaction network” class of models, essentially—and only broaden our view along the third axis.
Instead of concentrations, we’ll now consider the time-evolution of a probability distribution over the exact particle numbers.
A “state” will now be a distribution
This is a “stochastic” dynamical system, but will turn out to closely resemble a quantum-mechanical wave function, with the Master Equation corresponding to the Shrodinger Equation for many particles in a basis whose diagonal elements are the “occupation numbers” of each energy state, exactly like our
In quantum mechanics one might arrive at the same thing by first considering some
Following that analogy, we can represent a full state by an expression which looks like a wave function:
Here,
One could write the quantum-mechanical probability as
Our “Master Equation” will represent the time evolution of this distribution by a Hamiltonian-like operator:
The solution can be found for a given initial condition as a time-evolution operator which is just the matrix exponential of the generator
Now we’ll build it. First we need to represent our reactions in the occupation-number basis. We’ll use off the same example from the beginning of this essay:
Each reaction
How do we represent the rate of a reaction? Reaction
- The prior probability, of
- The rate constant
- The number of ways to choose all of the reaction’s inputs
We also have a condition that
Then the total rate of reaction
Our time-evolution generator will consist of one of such term for each initial state
This form implies that our generator matrix
The full Master Equation is:
We can isolate the generator of time-evolution
The Master Equation on Generating Functions
Now, rather than representing our state by a sum over occupation-number basis elements
You could motivate this in a few ways:
- Out of a general love for generating functions (like mine)
- Or, by analogy to the Rate Equation
- Or, by observing that falling powers
Guided by this observation, we’ll take our quantum-mechanical analogy even further by defining a “creation” operator
The implementation of
We’ll write each of these as a tuple over all species
We can also define a number operator
The
Note the quantum-mechanical analogy. For
Applying multiple
So we can also define the “falling power of the number operator
… and that is everything we need to represent the Master Equation as a time-evolution operator in the generating function representation:
This is a sum across reactions
Read this as:
- First, consume the inputs
- Then, in parallel:
- move to the new state
- subtract all of the probability from the original state
For comparison, here is the original original Master Equation, with
I prefer the operator version. There’s one fewer
Finally, in either representation, we can implement time-evolution by exponentiating this thing and acting on an arbitrary state:
Time Evolution as a Path Integral
Now we’ll briefly dip our toes into the next level down the ladder of abstraction.
One advantage of the operator formulation is that it lends itself to a path-integral-like interpretation, as follows. Observe that
Carrying out the powers leads to terms with sequences of
- the number of ways to choose candidates for those sequences: a product of terms
- the probability that those reactions occur independently, which gives a product of factors
- a correction
For example, if our network looks like this:
Then we have two “processess”
For this sequence the combinatorial term
We can draw diagrams for three of these combinations; the other 3 choose the same two inputs into

Observe that in each case one of the “1” particles passes through untouched, being affected by only the identity term of
These are something like Feynman diagrams. They’re mostly a conceptual aid at this level, but they could be useful when analyzing small-
Once again the most interesting result might be the light this can shed on quantum-mechanics through the analogy. It has always felt to me that QM was a tangled mess of concepts which, individually, are not all that complicated. Once you have an elementary example of each, the full theory ought to “factor”, with the particulars of quantum physics entering at clearly-delineated points. This could at least be an aid to pedagogy; of course any improvement to pedagogy can also improve the reach of pedagogy. If we dare hope for more, we might aim to better “compress” the body of physics knowledge better in the minds even of experts, letting all see further and more-easily grasp subtleties than in the current presentation. If!
-
Apparently, the coefficient in a derivative
Comments
(via Bluesky)