Table of Contents

1. Independence

In the previous post we saw that the entropy of a product distribution adds:

The above expression does not generalize to arbitrary joint distributions like or .

The entropy of a joint distribution is for for reason given its own name, the Joint Entropy, and has its own notation in terms of random variables:1

If and are independent, we can factor the joint probability into a product of marginals and the entropy adds as before. Spelling that out:

This is a bit reminiscent of the variance, which has a similar property for sums of independent distributions:

For non-independent distributions the variance behaves like a vector squared-norm , with the covariance as the corresponding inner product 2:

What happens to the entropy for non-independent distributions?

We can start by rewriting the joint distribution in terms of a conditional, which is exact:

where in the last line we’ve used the conventional notation for the conditional entropy

From this we can observe:

  • if is independent of , then and the conditional entropy reduces to the entropy of alone:

which recovers the additive property .

  • on the other hand, if is completely determined by , then takes a single value on each level set of . The marginal distribution is an indicator , which makes the entropy of every marginal distribution, and the conditional entropy, zero:

We see that, for completely-dependent , all of the variation and therefore all of the entropy belongs to alone. (Or equivalently to alone, if we marginalize in the other direction.) Intermediate degrees of independence then should interpolate between these results.

The joint entropy in always less than the independent case:

A number of the qualitative properties of entropy follow from these observations.

  • Correlations and “internal structure” always reduces entropy (while they tend to increase variances). In the extreme case of total dependence, they reduce a joint distribution of two variables into a single-variable distribution.
  • Expanding a sample space along a new dimension can only increase the entropy: .
  • Conditioning, such as with new “information” or “evidence”, can only reduce an entropy:
  • Entropy is “concave” over probability distributions: (this is an instance of Jensen’s Inequality)
  • Equivalently: whatever the entropy w.r.t. a specific distribution, uncertainty in the distribution itself will increases the entropy.

The last property is illustrated by the case of a biased coin distributed , whose probability of heads is known to be either or , with probabilities . The overall probability of heads is the weighted average , whose entropy is alway higher than the weighted average of the individual entropies

which follows from the concavity formula with ranging over , over , and over

We may conclude this discussion with one more concept, the mutual information, which is nothing but the difference between the joint entropy and the of the marginal entropies:

If we characterize as the information “in” which is not in , the last three expressions imply an interpretation of mutual information as the information “common to” both or .


2. Entropy as Measure?

A “Venn diagram” is useful to organize the preceding ideas:

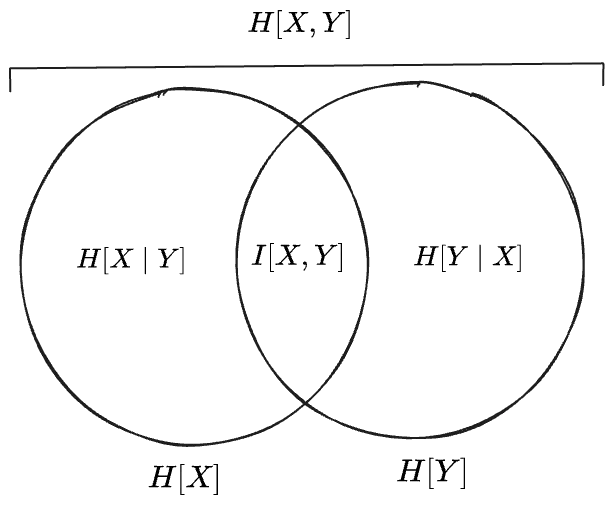
But, note, that while this diagram suggests an interpretation of entropy as the “measure” or “size” of some set—since Venn diagrams depict schematically the relationships between sets subsets—there exists no set of which these various entropy expressoins are measures. Instead we made the “Venn diagram” work by defining the mutual information to be exactly whatever was left over in after removing and .

Interestingly, though, Taylor series of the entropy expression around is

and the first term in this series is the measure of something. If we consider the distribution to be formed by binning a large set of elements into bins of size with , then the first term for some may be written

This expression admits an interpretation as the fraction of all pairs of elements from which relate one of elements of bin to one of the elements not in bin .

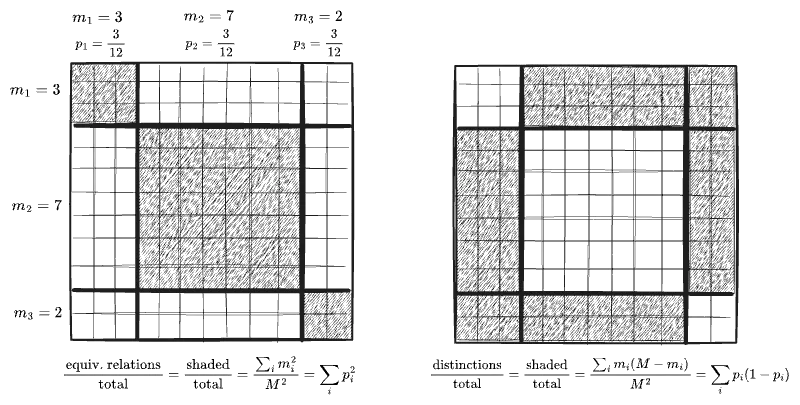
The full sum then represents the number of pairwise “distinctions”, as opposed to the “relations” (under the equivalence relation defined by the creation of the bins), as can be seen in the following visualization where is the distribution with weights .

Therefore the first term in this “series” expansion of does have the form of a probability; it is the measure of a subset of a space divided by that of the whole space:

The expression in this context has been called the logical entropy.3 I find this line of reasoning suggestive, but the idea feels incomplete. It suggests the later terms ought to admit interpretations as 3-distinctions, 4-distinctions, etc, but the is confounding. And, it is not really well-defined to take a Taylor expansion of with respect to all of the at once—they cannot all be close to at the same time!



  1. Elsewhere we’ll see the notation for the “cross entropy” of two distributions, with probabilities for arguments and an entirely different meaning. I prefer to use only probabilities like as arguments to entropy rather than random variables to avoid this kind of confusion. ↩

  2. The intuition here that independent distributions add “at right angles”, each contributing only its own randomness, while correlated distributions “constructively interfere”. See my post on variances for more. ↩

  3. An equivalent form is , which in other contexts is known as the Gini impurity or Simpson diversity index. ↩